What is the 'Golden Proportion'?
The Golden Proportion results from the division of a straight line in such a way that the shorter part is to the longer part as the longer part is to the whole. Each ratio equals 0.618:
S/L=L/(S+L)=0.618
Linear progressions and surface division by the same number are common in nature both geometrically and arithmetically. The geometrical progressions can be obtained by multiplying each term by 1.618 or dividing by 0.618:
1.000 x 1.618 = 1.618 or 1.000 : 0.618 = 1.618
1.618 x 1.618 = 2.618 or .618 : 0.618 = 2.618
2.618 x 1.618 = 4.236 or 2.618 : 0.618 = 4.236
In the arithmetic progression each term is the sum of the preceding two terms:
0.618 + 1.000 = 1.618
1.000 + 1.618 = 2.618
1.618 + 2.618 = 4.236
As can be seen here, the progression using the Golden number is unique because three different methods produce the same results.
Obviously, the Golden Proportion is not the only parameter that defines harmony and therefore beauty. However, numerous studies and experiments have demonstrated that this surface division creates an aesthetic appeal, independently from ethnic or civilization factors.
Golden Proportions have also been found in facial and dental elements:
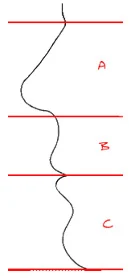
- The nasal height (A) is related to the maxillary height (B) as 1.000 : 0.618. The sum of nasal height and maxillary height (A + B) are related to the mandibular height (C) as 1.618 : 1.000.
- The mandibular height (C) is related to the maxillary height (B) as 1.000 : 0.618.
- The orofacial height (B + C) is related to the nasal height (A) as 1.618 : 1.000.
- Note that each ratio is 1.618.
Evidence of the application of Golden Proportion has existed since about 450 BC when Phidias made the Parthenon statues that seem to manifest this ratio. Plato, a few decades later, described five possible regular solids, some of which exhibit the Golden Proportion. Since then this ratio has gone through history as a symbol of aesthetics in architecture, paintings, design, mathematics, music, and nature. However, while coinciding with harmony and equilibrium, it is not a requirement for something to be considered beautiful.


